This is a series of 40 quarter-board Twixt puzzles, written by Alex Randolph. They are included in a booklet that comes with the Klee game company's version of the game. The puzzles are generally of increasing difficulty.

In each of these puzzles, you are asked to figure out how White can win locally. That means that White must be able to build an UNINTERRUPTED chain of linked pegs from anywhere in row A to anywhere in row L. BOTH sides must confine their pegs and links entirely within the quarter-board.

A move in Twixt consists of 2 stages:

1. Place one peg of your color in any vacant hole, EXCEPT in your opponent's border row. Note that there is no hole A1.
2. Link as many pairs of your pegs as you wish. A link may be placed between two pegs of your color ONLY when they are at opposite corners of a 6-holed rectangle, like a knight's move in chess, and no other link of either color blocks its way. You are permitted to remove your own links on your move, if you wish, prior to placing any.

Puzzle #1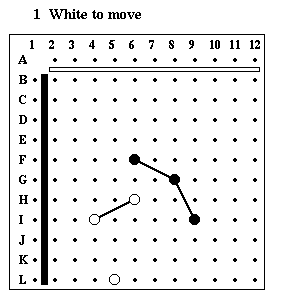

Solution

Puzzle #2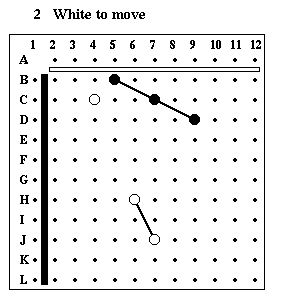

Solution

Puzzle #3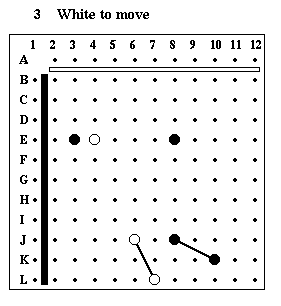

Solution

Puzzle #4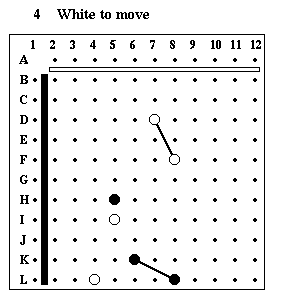

Solution

Puzzle #5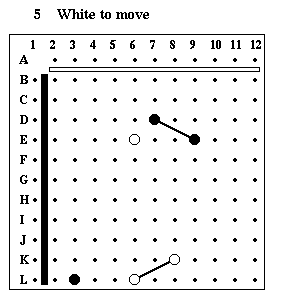

Solution

Puzzle #6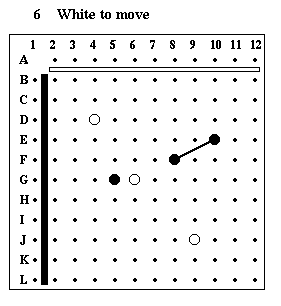

Solution

Puzzle #7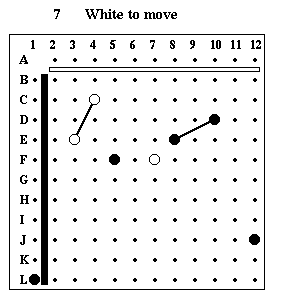

Solution

Puzzle #8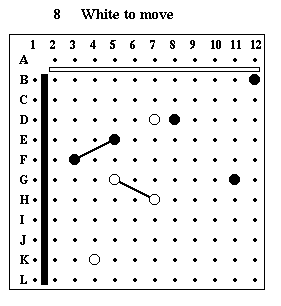

Solution

Puzzle #9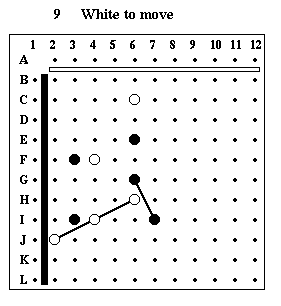

Solution

Puzzle #10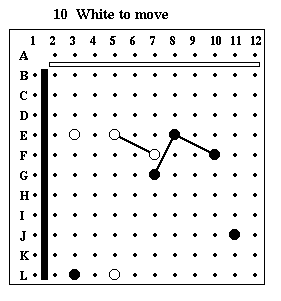

Solution

Puzzle #11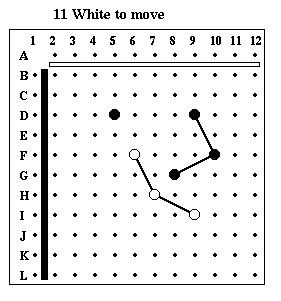

Solution

Puzzle #12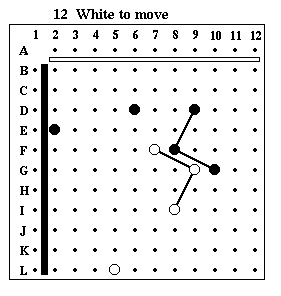

Solution

Puzzle #13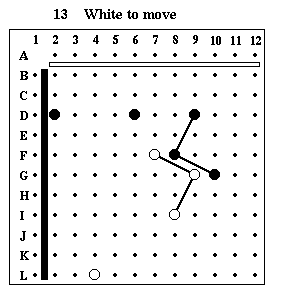

Solution

Puzzle #14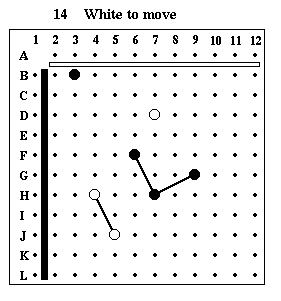

Solution

Puzzle #15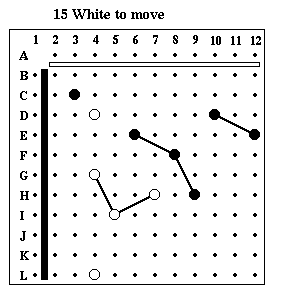

Solution

Puzzle #16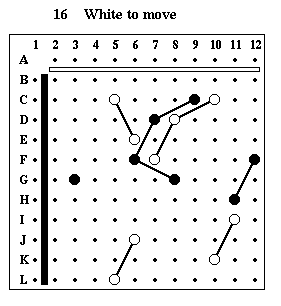

Solution

Puzzle #17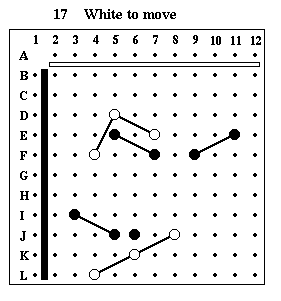

Solution

Puzzle #18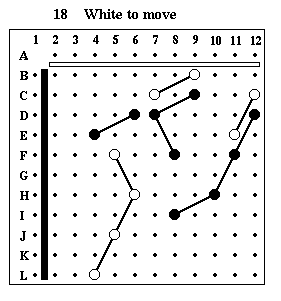

Solution

Puzzle #19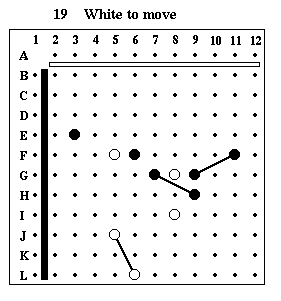

Solution

Puzzle #20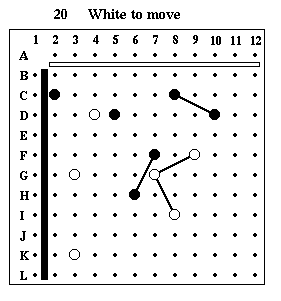

Solution

Puzzle #21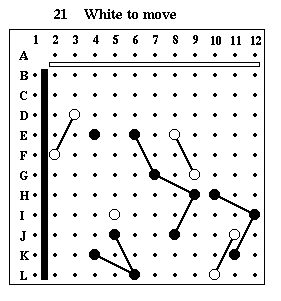

Solution

Puzzle #22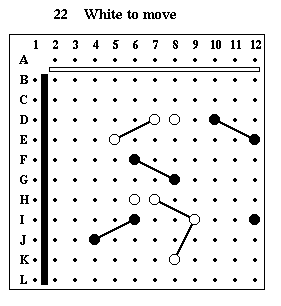

Solution

Puzzle #23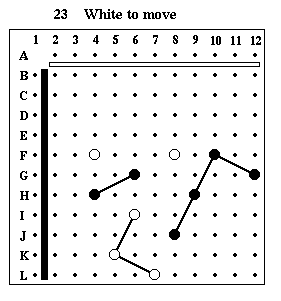

Solution

Puzzle #24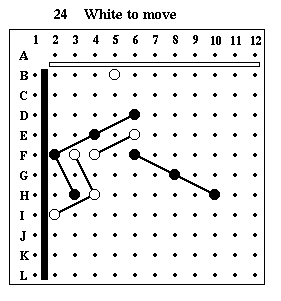

Solution

Puzzle #25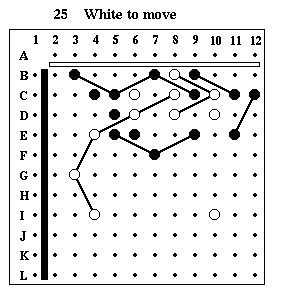

Solution

Puzzle #26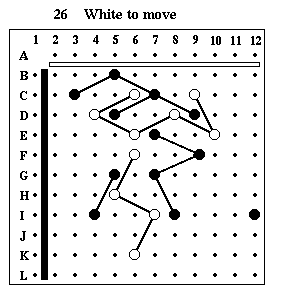

Solution

Puzzle #27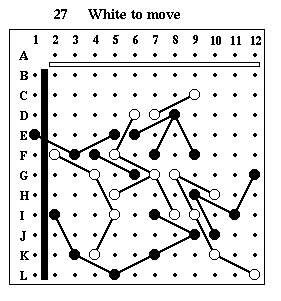

Solution

Puzzle #28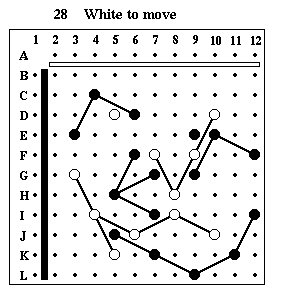

Solution

Puzzle #29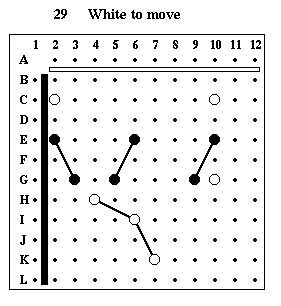

Solution

Puzzle #30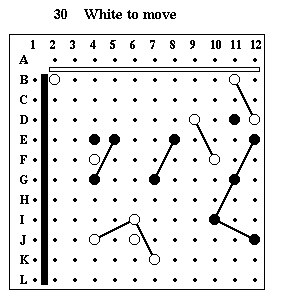

Solution

Puzzle #31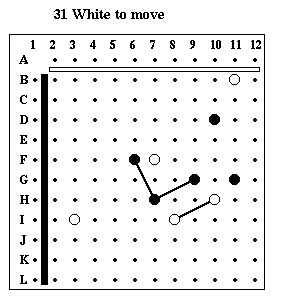

Solution

Puzzle #32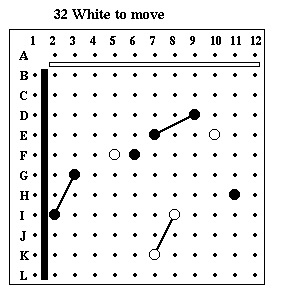

Solution

Puzzle #33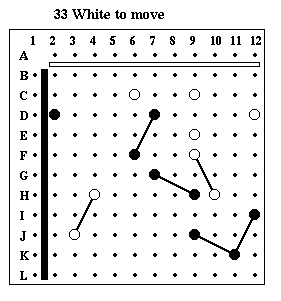

Solution

Puzzle #34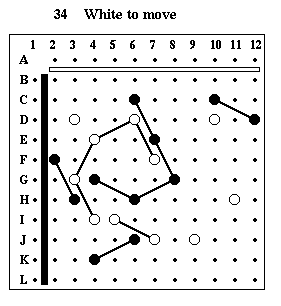

Solution

Puzzle #35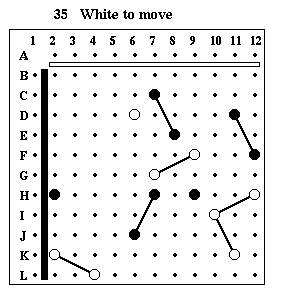

Solution

Puzzle #36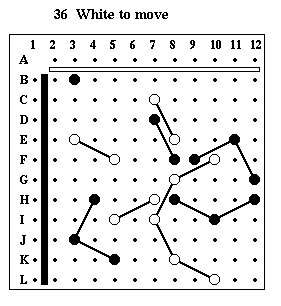

Solution

Puzzle #37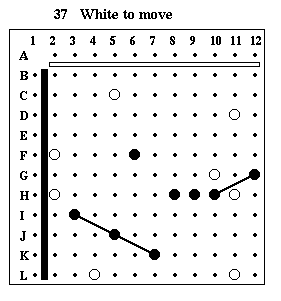

Solution

Puzzle #38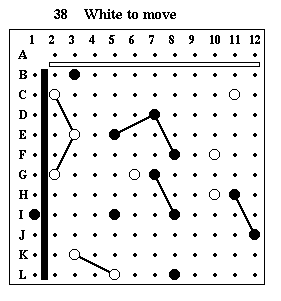

Solution

Puzzle #39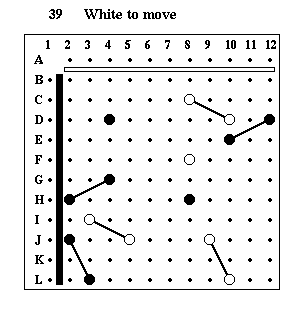

Solution

Puzzle #40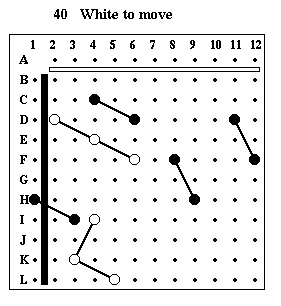

Solution